Quem não gosta de ouvir histórias? As histórias podem nos fazer sonhar, experimentar sensações, refletir, viajar no tempo e no espaço! Então, por que não contar histórias nas aulas de matemática? Sim, histórias da matemática! Elas falam sobre como a matemática nasceu e de como os homens resolveram os problemas da antiguidade.
A história tem poder motivador, já que desperta o interesse do aluno no conteúdo a ser estudado e, por conseguinte, auxilia no processo de ensino-aprendizagem da matemática. O professor pode criar estratégias metodológicas e atividades significativas a partir da história da matemática, além de ter a possibilidade de esclarecer muitas dúvidas dos alunos acerca de procedimentos e processos matemáticos. Vejamos algumas histórias ...
A história da numeração pode dar o pontapé inicial ao trabalho. O surgimento do nosso sistema de numeração e das numerações de outros povos é bastante interessante e possibilita desenvolver um trabalho interdisciplinar, principalmente com a história e a geografia. As histórias relacionadas às frações, geometria e medidas também propiciam uma abordagem histórica bem rica. No que se refere à numeração, de acordo com Imenes, tudo indica que foram os pastores, com o uso de pedrinhas, que realizaram as primeiras contagens. De manhã, quando as ovelhas saiam para o pastoreio, o pastor separava uma pedrinha para cada animal e formava um montinho com elas.
No final, do dia, conforme retornava cada animal, o pastor retirava uma pedrinha do montinho. A sobra de pedrinhas era sinal de que alguns animais não haviam voltado e a falta de alguma poderia indicar a que o rebanho teria aumentado.
Imenes enfatiza que a origem da palavra cálculo vem da palavra latina calculus, que significa pedrinha e que, provavelmente, a origem da palavra calcular seja: contar com pedrinhas.
Além de pedras o homem utilizou outros recursos para auxiliá-lo nas contagens, tais como, marcas em ossos ou madeira e nós em cordas. Também o corpo humano foi usado com esse propósito; tanto é verdade que a palavra dígito, do latim dígitus que significa dedo, é utilizada até hoje como sinônimo de algarismo. Para contar grandes quantidades, o homem sentiu a necessidade de criar um sistema de numeração. Assim, de acordo com Imenes, vários povos, como os Egípcios (4.500 a.C a 300 a.C) e os Romanos (500 a.C a 500 d.C), criaram sistemas numéricos, cada qual com características próprias. 
O período em que essas civilizações floresceram pode provocar discussões na sala de aula a respeito do calendário cristão, utilizado por nós, e sobre fatos ocorridos nos anos anteriores e posteriores ao nascimento de Jesus. Cabe esclarecer que, no calendário cristão, os anos são contados tendo como referência o ano do nascimento de Cristo. Assim sendo, neste calendário não há ano zero e o ano 1 é o primeiro ano da era cristã. Os anos anteriores ao nascimento de Jesus trazem a abreviação a.C. e os anos posteriores levam a indicação d.C.
Gutierre sugere que o professor trabalhe com mapas geográficos e com uma linha de tempo para situar os alunos no tempo e no espaço. Segundo a autora, a experiência de convidar a turma de alunos para realizar uma viagem pelo tempo e pelo espaço é fator de entusiasmo e as “paradas” em diferentes locais da antiguidade favorece a abordagem de diferentes assuntos.
A civilização egípcia desenvolveu-se às margens do Rio Nilo onde, ainda hoje, é o Egito. A grandiosidade das pirâmides, templos e monumentos egípcios, bem como a vida e a cultura desse povo, sempre despertaram a curiosidade da humanidade. Os egípcios embalsamavam os mortos, pois acreditavam numa vida após a morte; também colocavam nos túmulos objetos de valor da pessoa falecida.
De acordo com Guelli, a decifração dos hieróglifos (inscrições em monumentos e tumbas) permitiu que os cientistas descobrissem que os egípcios utilizavam sete números-chave representados por sete figuras. Qualquer outro número era escrito combinando-se os números-chave, sendo que a ordem em que os símbolos eram escritos não tinha importância. Eles contavam, como nós hoje, formando grupos de dez; sendo assim, o sistema egípcio antigo tinha base dez.
Para trabalhar com o sistema de numeração egípcio, SÃO PAULO sugere que o professor, como atividade introdutória, instigue a turma a descobrir o funcionamento dessa numeração a partir da análise de inscrições egípcias e de algumas pistas. Os exemplos abaixo dão uma ideia da proposta:
A partir da descoberta das leis do sistema egípcio, os alunos podem aventurar-se a representar outras quantidades utilizando o método e, até mesmo, estabelecer relações entre os sistemas egípcio e decimal.
Assim como os egípcios, os romanos também criaram seu próprio sistema de numeração que é ainda utilizado nos dias de hoje. A civilização romana, conforme destaca Guelli, foi a mais importante de todas as civilizações antigas.
Tinha como centro a cidade de Roma e seus habitantes enfrentaram todos os tipos de guerras. As batalhas eram travadas na conquista de outros povos ou na defesa aos ataques dos inimigos. Os romanos conseguiram aumentar seu território, conquistando a Península Itálica e o restante da Europa, o norte da África e uma parte da Ásia.
O sistema romano também tem base dez e se parece muito com o egípcio. Aliás, os romanos foram muitos espertos na invenção de sua numeração pois, além da praticidade e eficiência do seu sistema, não criaram símbolos novos para pois utilizaram as letras do alfabeto.
No princípio, de acordo com Mori; Onaga, os símbolos romanos estiveram associados ao registro da contagem de votos em eleições, que era feito com o uso de traços. Para os números de um a quatro eram utilizados um, dois, três ou quatro traços; o cinco era escrito com cinco traços cortados por outro inclinado e o dez era formado por cinco traços cortados por dois inclinados.
Com o passar do tempo, a fim de facilitar a leitura e escrita dos números, os símbolos romanos foram sendo modificados e simplificados. Imenes destaca que, para muitos especialistas, o cinco romano (V), por exemplo, pode ter-se originado da figura de uma mão aberta.
Assim como proposto no sistema egípcio, os alunos podem tentar descobrir as regras de formação dos números romanos a partir da análise de alguns números.
Dicas e questionamentos do professor auxiliarão a perceber as leis do sistema:
I – 5 V – 5 X – 10 L – 50 C – 100 D – 500 M – 1000
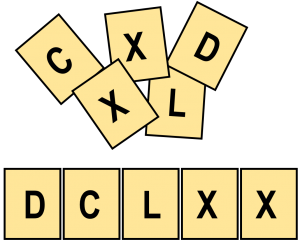
Para este jogo é necessário providenciar, para cada grupo de 4 alunos, 5 cartas de cada um dos sete símbolos da numeração romana; serão, no total, 35 cartas. As cartas são embaralhadas e cada aluno do grupo toma 5 cartas para si. O objetivo do jogo é formar um número com cinco ou menos cartas e apresentá-lo ao grupo. Assim, cada jogador analisa suas cartas e organiza-as sobre a mesa dispondo-as à sua frente, de forma a mostrar o maior número romano que conseguir.
Todos os jogadores deverão ler em voz alta seus números e aquele que apresentar o maior número é o vencedor da rodada. As cartas são embaralhadas novamente e outras rodadas semelhantes ocorrem. Combina-se, antecipadamente, qual será o número total de rodadas.
Não foram somente as civilizações egípcia e romana que criaram sistemas de numeração próprios. Outros povos também o fizeram e os diferentes sistemas criados apresentavam vantagens e desvantagens. A civilização babilônia, que há mais de 4000 anos habitava a Mesopotâmia (hoje região próxima ao Iraque), inventou um sistema numérico de base sessenta que nos influencia ainda hoje na divisão da hora em 60 minutos, do minuto em 60 segundos e da circunferência em 360 graus (TELECURSO).
Porém, nenhum dos sistemas numéricos existentes era suficientemente eficiente. Foi necessário o aparecimento de outro que facilitasse os cálculos e o registro dos números. O tal sistema pretendido foi criado pelos hindus e divulgado ao mundo pelos árabes; chama-se sistema de numeração decimal ou indo-arábico e é utilizado por nós até hoje.
Segundo Imenes, a origem do nosso sistema é muito antiga. Surgiu na Ásia, no vale do Rio Indo, onde é o Paquistão hoje, local que era habitado pela civilização hindu. O povo hindu desenvolveu-se há mais de quatro mil anos e suas ruínas revelaram uma civilização bastante avançada, cuja população construiu casas com tijolos de barro, organizou povoados com ruas calçadas, fornecimento de água e canalização de esgotos. Porém, por volta de 1500 a.C. esse povo desapareceu, muito provavelmente devido às invasões sofridas.
Os hindus criaram um sistema posicional, de base dez, que utiliza apenas os símbolos 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Os árabes entraram em contato com o sistema numérico, adotaram-no e o levaram à Europa através de suas invasões àquele continente.
Segundo Guelli, um brilhante matemático árabe, chamado Al-Khowarizmi, escreveu um livro explicando como funcionava a numeração dos hindus e, dessa forma, revelou ao mundo a grande descoberta. Do nome desse árabe originou-se da palavra latina algorismus e dessa o nome “algarismo” usado para designar os signos numéricos.
Depois de conhecer a história da nossa numeração, os alunos poderão analisar alguns números para observar as características do sistema (valor absoluto e valor relativo, leitura, escrita, etc.). Atividades que solicitem a escrita de um mesmo número nos sistemas egípcio, romano e decimal, tal como a que segue, favorecerão a comparação das diferentes numerações.
Como atividade extra, o professor poderá propor aos alunos que, em grupos, criem um sistema de numeração próprio (símbolos, funcionamento, características) e depois o expliquem aos colegas.
Outra história interessante a ser contada aos alunos é a que relata o nascimento da geometria. Segundo Mori; Onaga, há mais de 4500 anos, no antigo Egito, a geometria surgiu devido aos problemas de medição de terras.
O Rio Nilo, que banha o Egito, transbordava na época das cheias e, a cada inundação, destruía as cercas usadas para a demarcação dos terrenos. Quando as águas baixavam, os egípcios dividiam novamente os terrenos utilizando as medidas tiradas antes da enchente. Naquela época, os egípcios já utilizavam triângulos para marcar cantos retos.
Os gregos, que aprenderam geometria com os egípcios, também ajudaram a desenvolve-la; aliás, foram eles que deram o nome “geometria” sendo que geo significa terra e metria tem o significado de medida. A história dos egípcios e a demarcação de suas terras devido às cheias do Rio Nilo também justifica a criação das medidas de comprimento e das frações.
Machado relata que os agricultores do Egito tinham que pagar impostos ao faraó pela extensão de terra que possuíam. Por causa disso, os agrimensores do faraó mediam as terras com cordas constituídas de nós igualmente espaçados; a distância de um nó a outro era a unidade de medida. Ao esticar as cordas mediam grandes distâncias observando-se quantas vezes a unidade de medida cabia no comprimento a ser medido.
De acordo com Mori; Onaga, ao medir as terras com as cordas, os egípcios nem sempre encontravam um número inteiro como resultado, ou seja, muitas vezes a medida não podia ser representada por um número natural porque a unidade de medida não cabia exatamente no comprimento que estava sendo medido. Então, eles sentiram a necessidade de criar um número que representasse uma parte ou uma porção da unidade: a fração.
Guelli enfatiza que os egípcios utilizavam apenas frações com numerador igual a 1 (frações unitárias) sendo que, para escrevê-las, desenhavam um símbolo oval sobre o denominador. As outras frações que não tinham numerador 1 eram obtidas através da soma das frações unitárias e, por isso, o cálculo com frações tornava-se muito difícil.
Para escrever, por exemplo, um número maior que 111 e menor que 112 sem usar frações, passou-se por um longo período até o surgimento de uma ideia tremendamente fantástica e simples: colocar uma vírgula no fim de um número natural e continuar escrevendo algarismos também depois da vírgula. Conforme destacam Imenes, Jakubovic e Lellis, usando-se a lógica do sistema de numeração decimal, a posição seguinte à vírgula tem o valor da posição das unidades dividido por 10; ou seja, é a casa dos décimos. A escrita dos números naturais podia avançar o quanto quisesse, pelas dezenas, centenas, milhares, etc. e a vírgula permitiu que se avançasse, também, no sentido oposto.
No que se refere às medições de terras, os próprios egípcios tinham outras formas para medir pequenas extensões. Eles utilizavam o cúbito ou côvado (distância do cotovelo até a ponta do dedo médio) e até construíram bastões com comprimento igual a 1 cúbito para auxiliar na tarefa. O uso de bastões facilitava também o desenvolvimento do comércio.
Outros povos também tinham seus padrões de medida: eram utilizados palmos, polegadas, pé, jardas, etc., medidas essas originadas do corpo humano. Porém, conforme o mundo se desenvolvia e as relações comerciais entre os povos ia aumentando, a existência de diferentes padrões criava confusões, pois haviam cúbitos, palmos, pés, etc., de diferentes tamanhos. Foi então que os homens sentiram a necessidade da existência de uma unidade padrão de medida.
De acordo com o Telecurso 2000, no final do século XVIII um grupo de cientistas reuniu-se na França e escolheu o metro como medida padrão. O metro foi reconhecido internacionalmente e, a partir dessa data, passaram a existir instrumentos com a medida do metro no mundo todo.
Toledo; Toledo (1997) esclarecem que a palavra metro vem do grego, metron, e significa medida. Segundo os autores “o metro é um múltiplo do comprimento de onda do gás criptônio, presente na atmosfera. Esse comprimento de onda pode ser obtido em qualquer país e é fixo”.
Os alunos podem sentir na própria pele a confusão que o uso das unidades de medida antigas causava a partir de atividades em que sejam convidados a medir a largura ou comprimento da sala com pés ou passos; o comprimento da classe com polegadas ou palmos e a largura do quadro com jardas ou cúbitos. Na comparação dos resultados obtidos ficará claro que as medidas encontradas variam de pessoa para pessoa. Certamente, o estudo do metro, de seus múltiplos e submúltiplos ficará bem mais atrativo após a realização de atividades semelhantes às sugeridas e do conhecimento dos fatos históricos relacionados ao surgimento das medidas.
Uma última história que será abordada neste artigo refere-se a origem do ângulo. Ledur; Enriconi; Woff relatam o seguinte: “Houve um tempo em que os antigos acreditavam que o Sol girava em torno da terra numa órbita circular e levava 360 dias para dar uma volta completa. Assim, a cada dia de órbita percorrida correspondia a 1 grau, isto é, 1/360 da circunferência. Esta unidade passou a ser a unidade de medida de um ângulo e se denominava grau (1°). Hoje sabemos que a Terra é que gira em torno do Sol, a órbita não é circular, mas elíptica, no entanto, o sistema sexagesimal dos babilônios foi mantida”.
Então, em algum momento da história, os homens chegaram a pensar que o ano durasse 360 dias e, mesmo depois de concluírem que esse fato não era verdadeiro, resolveram manter o número 360 para algumas medidas. Assim, a invenção do grau foi um feito dos babilônios. Numa abordagem introdutória sobre ângulos é interessante associá-los a giros de volta inteira, meia volta e um quarto de volta, tendo como referência o próprio corpo. A história contada anteriormente justifica o motivo pelo qual são associados a esses giros os ângulos de 360º, 180º e 90º, respectivamente.
BRASIL. Parâmetros Curriculares Nacionais: Matemática. 2. ed. Rio de Janeiro: DP & A, 2000. 3.v.
BORGES, Pedro Augusto. Matemática 5ª série: melhoria do ensino de ciências e matemática. Ijuí: Unijuí, 1991.
FUNDAÇÃO ROBERTO MARINHO; FEDERAÇÃO DAS INDÚSTRIAS DO ESTADO DE SÃO PAULO; CENTRO DAS INDÚSTRIAS DO ESTADO DE SÃO PAULO; SERVIÇO NACIONAL DE APRENDIZAGEM COMERCIAL; SERVIÇO NACIONAL DE APRENDIZAGEM I. Matemática: 1º grau. São Paulo: Globo, 1994. 1 v. (Telecurso 2000 : 1º grau).
GUELLI, Oscar. Contando a história da matemática: a invenção dos números. São Paulo: Ática, 1992.
GUTIERRE, Liliane dos Santos. Inter-relações entre a História da Matemática, a Matemática e sua aprendizagem. 2003.
Dissertação (Mestrado em Educação) – Universidade Federal do Rio Grande do Norte, Natal, 2003. IMENES, lUiz Márcio. Os números na história da civilização. São Paulo: Scipione, 1989.
IMENES, Luiz Márcio. A numeração indo-arábica. São Paulo: Scipione, 1989.
IMENES, Luiz Márcio; JAKUBOVIC, José; LELLIS, Marcelo C. Geometria. 14. ed. São Paulo: Atual, 1992.
LEDUR, Elsa Alice; ENRICONI, Maria Helena S.; WOLFF, Rosane. Refletindo o ensino da geometria. In RIO GRANDE DO SUL. Secretaia de Educação. Educação para crescer: Projeto Melhoria da Qualidade de Ensino: Matemática 1º grau. Porto Alegre: [s.n.],1993.
MACHADO, Nilson José. Medindo comprimentos. 2.ed. São Paulo: Scipione, 1988. MENDES, Iran Abreu. Investigação histórica no ensino da matemática. Rio de Janeiro: Ciência Moderna, 2009.
MIGUEL, Antonio; MIORIM, Maria Ângela. História na Educação Matemática: propostas e desafios. Belo Horizonte: Autêntica, 2008.
MORI, Iracema; ONAGA, Dulce Satiko. Para aprender matemática: 5ª. 3. ed. São Paulo: Saraiva, 1991. SÃO PAULO (Estado) Secretaria de Educação. Coordenadoria de Estudos e Normas pedagógicas. Experiências Matemáticas: 5ª série. São Paulo: SE/CENP, 1998.
TOLEDO, Marília; TOLEDO, Mauro. Didática de matemática: como dois e dois: a construção da matemática. São Paulo: FTD, 1997.
27/01/2017
12/02/2024
Para auxiliar o professor no preparo de aulas envolvendo o sistema monetário, elaborei um e-book que contempla 18 jogos e atividades dinâmicas e atrativas, direcionados aos estudantes do 1º ao 5º anos do ensino fundamental.
04/09/2023
Este jogo vai auxiliar as crianças do 1º e 2º anos do ensino fundamental na memorização dos fatos básicos das subtração. É muito fácil de implementar e envolve apenas cartinhas e dados.
01/08/2023
Criei o jogo da reta numérica para auxiliar as crianças do 1º e 2º anos a localizarem números na reta de forma lúdica. Os alunos vão jogar em duplas, trios ou quartetos utilizando apenas a reta de papel e um dado.
Este site usa cookies para proporcionar uma melhor experiência para você. Ao prosseguir, você concorda com nossas Políticas de Cookies e de Privacidade. Saiba mais
